The “Differential Data” tab

At this tab you will extract the high-order data (Gradients and Hessians) that are necessary in order to calculate the self-optimizing control structures using the exact local method from [2].

The high-order data is calculated with analytical expressions derived by [26] and [3], using the kriging metamodel built for the reduced space problem.

The aforementioned procedure is encapsulated in this tab. You will be able to:

  • Generate the gradients and hessians, and inspect them.

  • Remove any CV candidate from the list of candidates if you want.

Here is an overview of this tab, before you start using it:

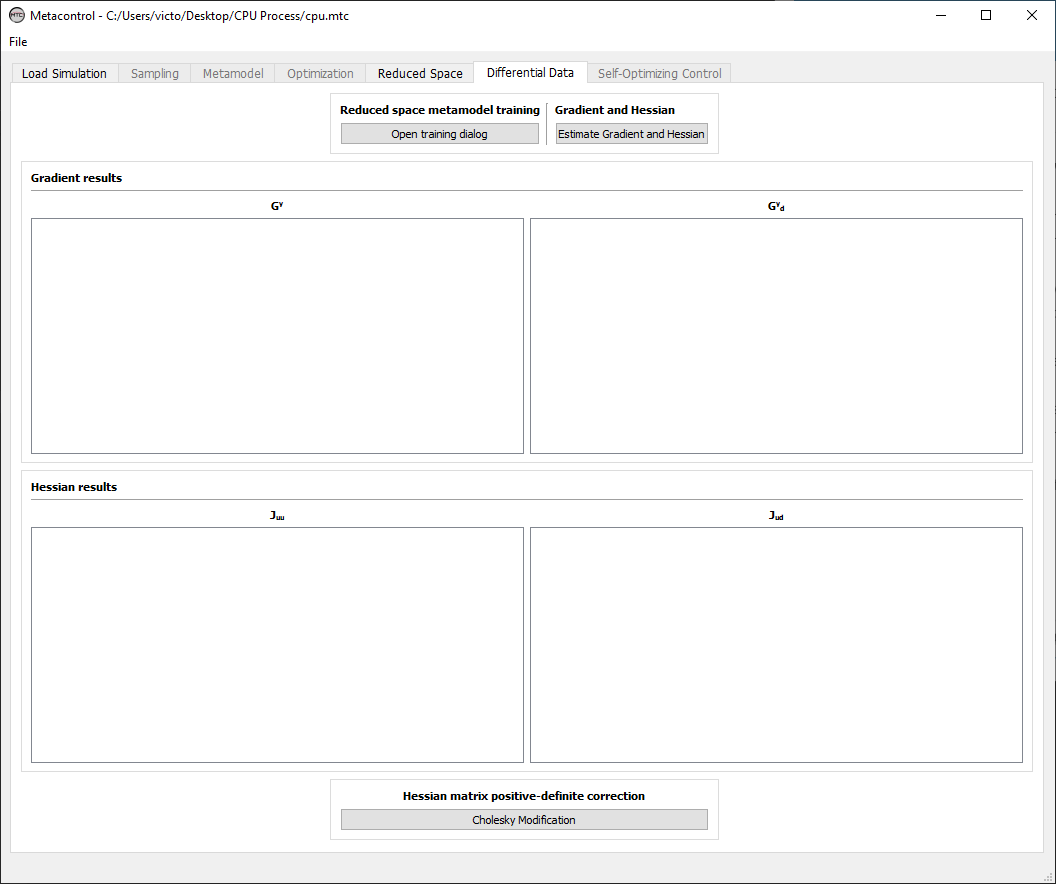
../_images/diff_data_main.png

Fig. 60 Differential Data tab.

There are four main panels on this tab

  • Reduced space metamodel training Panel

  • Gradient and Hessian estimation Panel

  • Gradient results panel and Hessian results panel

Reduced space metamodel training Panel

Under this panel, you are able to click on “Open training dialog” in order to configure your reduced-space kriging metamodel.

Configuring your kriging metamodel

Click on “Open training dialog”:

../_images/diff_data_training_dialog.png

Fig. 61 Opening the kriging training dialog window.

You will notice that the window that appears to you is exactly the same from The “Metamodel” tab. Therefore the process of configuring your reduced-space kriging metamodel is essentially the same.

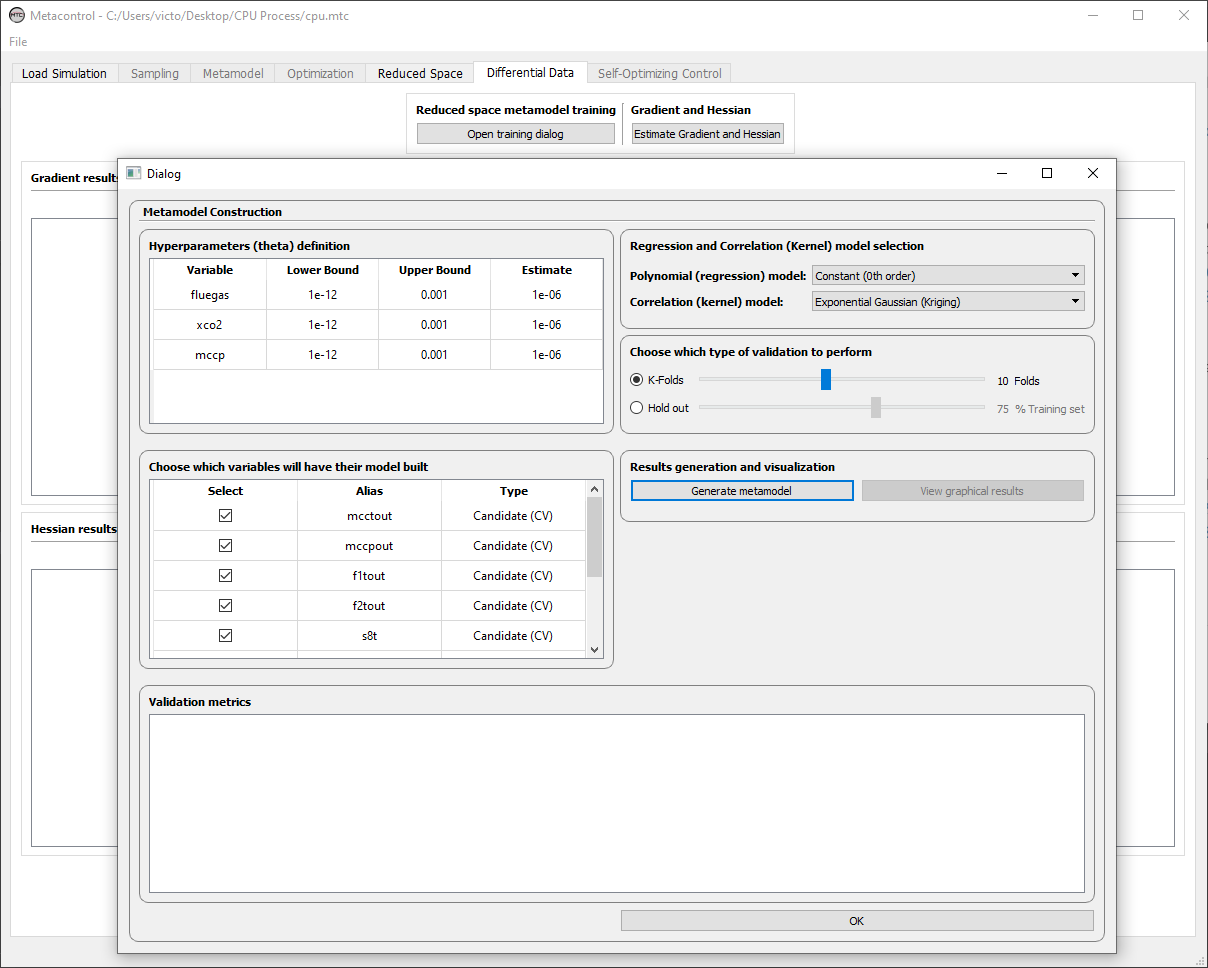
../_images/diff_data_training_dialog_window.png

Fig. 62 Training dialog window.

Important

At the training dialog window, you will notice that only the Candidates that were not active constraints are considered now. This happens because Metacontrol automatically removes the variables that are nominally active (MVs and CVs) based on the previous tab (Reduced Space tab). In addition, you can remove any of the remaining CVs, if you want. Just de-select the box of the variable you want to remove:

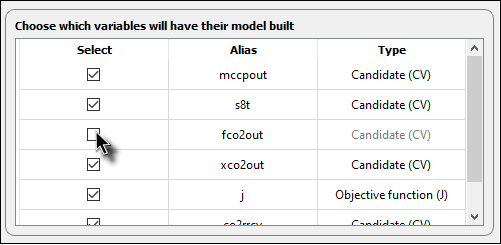
../_images/diff_data_remove_cvs.png

Fig. 63 Removing one variable from the CV candidates list (fco2out in this example).

After configuring the hyperparameters estimates, choosing which CVs will be taken into acount in your metamodel, you can click on “Generate metamodel” in order to inspect the validation metrics of your metamodel.

Acessing performance of your reduced-space metamodel

For the reduced-space metamodel, one additional metric has been added in order to help you to evaluate the robustness of the metamodel generated. It corresponds to the objective function of the maximum likelihood estimation from the work of [26]. Values under 1e-5 will give robust estimation of the gradients and hessians. (Check Our papers and the Theoretical Backgrounds section where we give some examples and discuss the theoretical background in detail)

../_images/diff_data_dace_function.png

Fig. 64 Evaluating reduced space kriging metamodel estimation capabilities. Highlighted in blue, the value of the optimized objective function value, that results in the optimal hyperparameters estimation.

Gradient and Hessian estimation Panel

After configuring the kriging metamodel options under the training dialog window, you can click on “Estimate Gradient and Hessian”, to generate the high-order data.

../_images/diff_data_high_order_data_gen.png

Fig. 65 Generating high-order data.

Gradient results panel and Hessian results panel

After performing the previous step, you will notice that the panels for Gradients and Hessians are now completed:

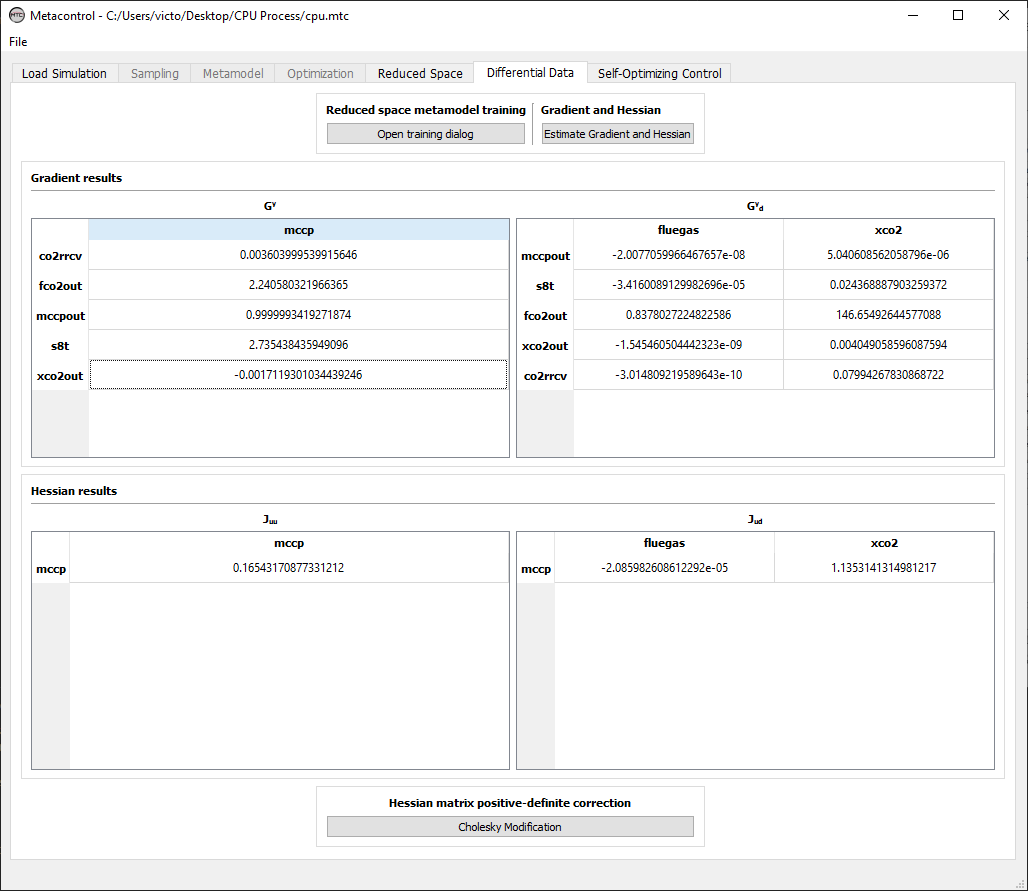
../_images/diff_data_completed.png

Fig. 66 Generating high-order data.

If you take a closer look, you will notice that the matrices are in a Dataframe format, making them easy to ready and to understand each element of the matrices generated. Note that the elements are indexed using the aliases that you created. For example, the gain between the unconstrained degree of freedom (mccp) and one CV candidate (co2rrcv) is easily read:

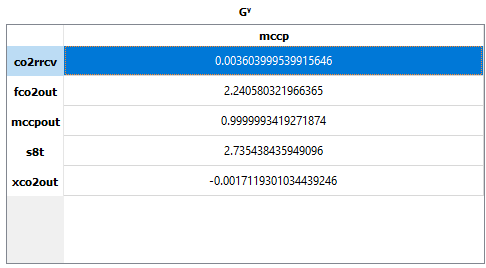
../_images/diff_data_reading_gains.png

Fig. 67 Generating high-order data.

The same is true for every element of the gradients and hessians calculated.

After the procedure here described, you can go to the last tab: Self-Optimizing Control.