The “Self-Optimizing Control” tab

At this tab the self-optimizing control structure selection is made. You will be able to:

  • Provide the expected disturbances and implementation/measurement magnitudes to be taken into account in your study

  • Inform Metacontrol how many best (that incurs in the lowest loss) structures do you want to analyze for each possible control structure subset size

  • Inspecting in ascending and descending order all evaluated control structures

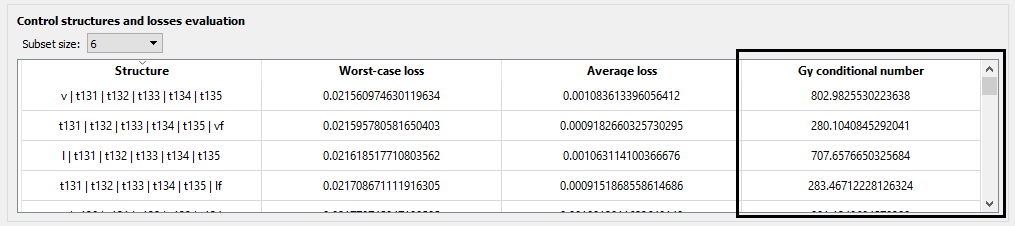
  • Inspect the condition number of each control structure

  • Inspect linear combinations of controlled variables, if you chose to analyze more CV candidates than the unconstrained degrees of freedom available.

This tab looks like the picture below, before you start to fill the necessary data:

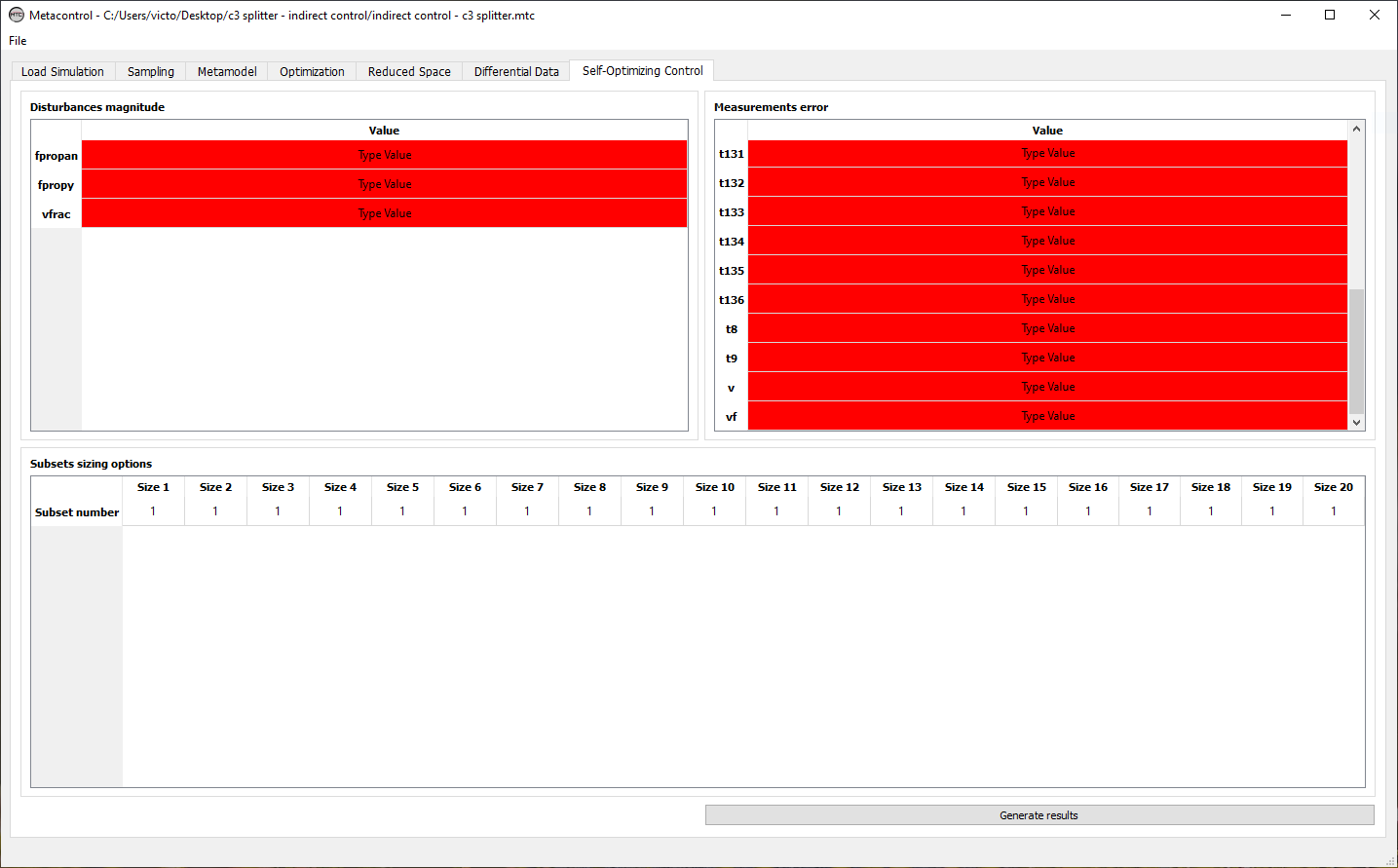
../_images/soc_main_tab_before_completion.png

Fig. 68 Metacontrol “Self-Optimizing Control” tab.

The forms are red because you need to supply the data for the disturbances and implementation/measurement errors magnitudes.

There are three panels at this tab:

  • Disturbances magnitude panel

  • Measurement error panel

  • Subsets sizing options panel

Disturbances magnitude panel

At this panel, you will inform to Metacontrol the expected magnitude of the disturbances. As an example, see the figure below, where it was considered 10% of the nominal value for the variables fpropan, fpropy and vfrac:

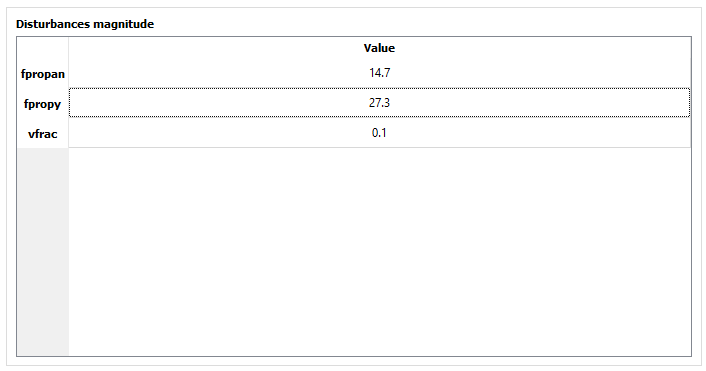
../_images/soc_disturbances_magnitude_panel.png

Fig. 69 Entering disturbances expected magnitudes.

Measurement error panel

At this panel, you will enter the expected implementation/measurement error. For the example on the figure below, it was considered 0.5°C for temperature measurements and 0.001 for flow measurements.

../_images/soc_measurement_error_panel.png

Fig. 70 Entering measurement error expected magnitudes.

Subsets sizing options panel

At this panel you will determine how many best control structures will be reported to you by Metacontrol, for each possible subset size:

../_images/soc_subset_sizing_options_panel.png

Fig. 71 Entering measurement error expected magnitudes.

Metacontrol and the maximum number of possible control structures for each subset size

Metacontrol automatically calculates the maximum number of possible control structures for each subset size.

For the example shown in the previous figure, there are 20 CV candidates and two unconstrained degrees of freedom available. For a single measurement policy (using one single CV candidate for each MV) there are

\[(20! / 2!) = 20!/(2! \times (20-2)!) = 190\]

possible control structures. If the user tries to evaluate 191 (which is impossible), Metacontrol will prevent him from doing this:

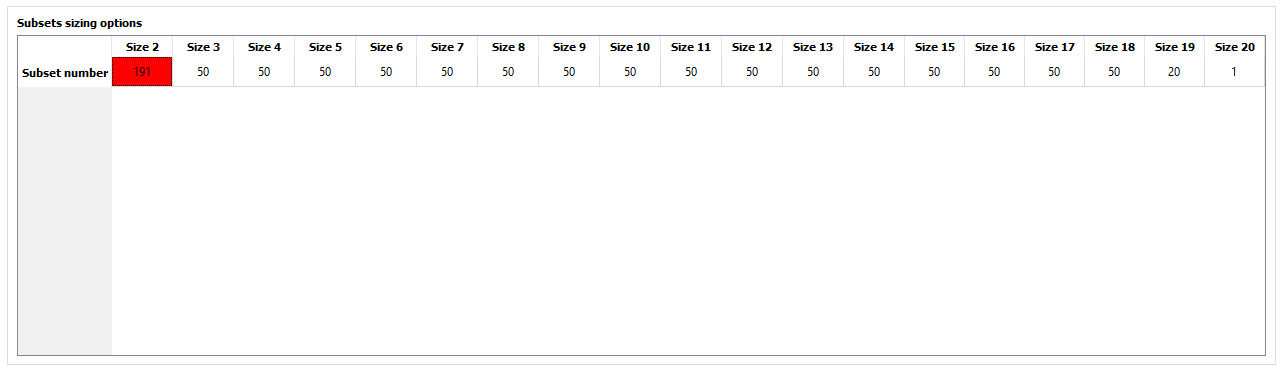
../_images/soc_subset_sizing_impossible.png

Fig. 72 Metacontrol avoiding impossible evaluations.

Analyzing your results

After completing this tab with the all necessary data, you can click on “Generate Results”, and a window will appear:

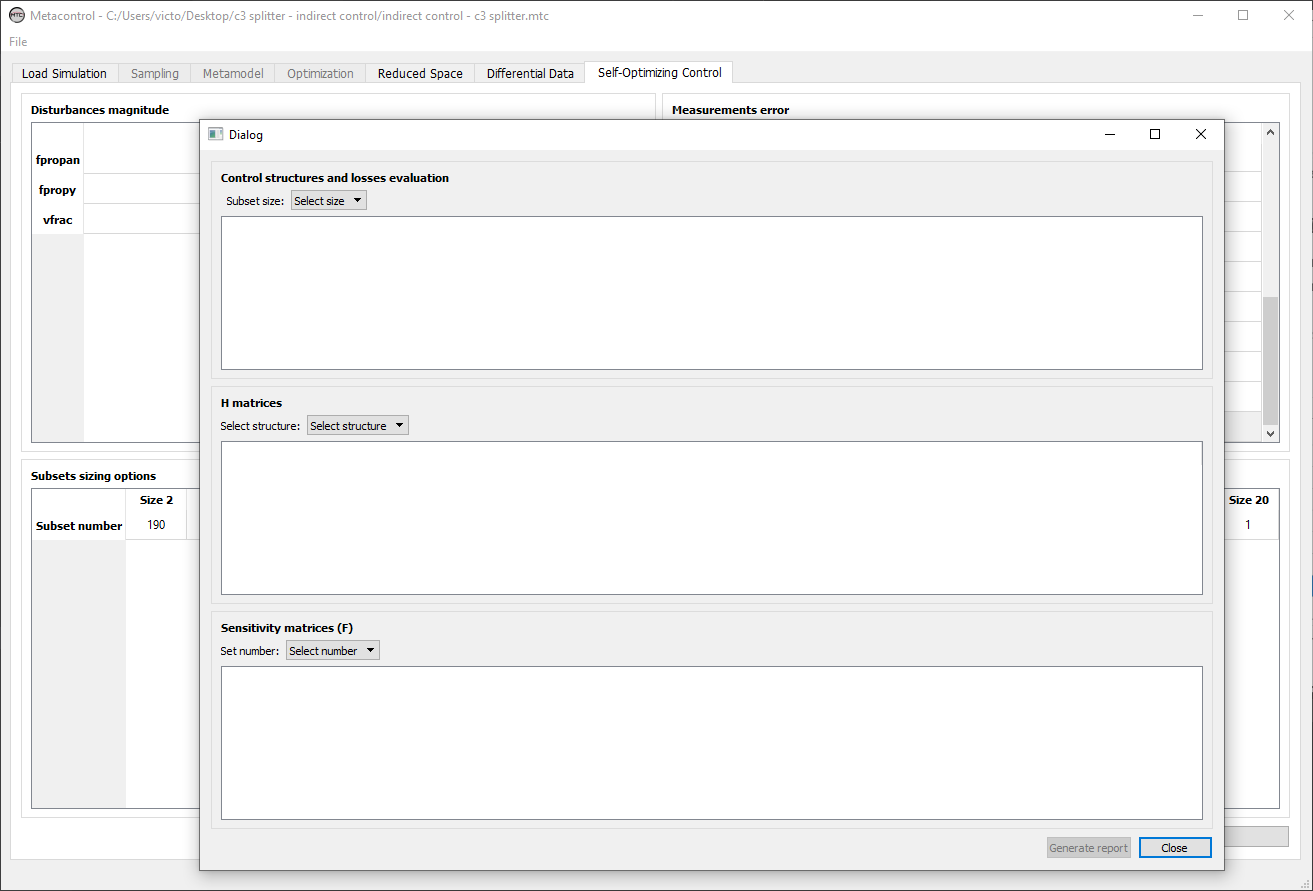
../_images/soc_results_review.png

You can select which subset size you want to analyze:

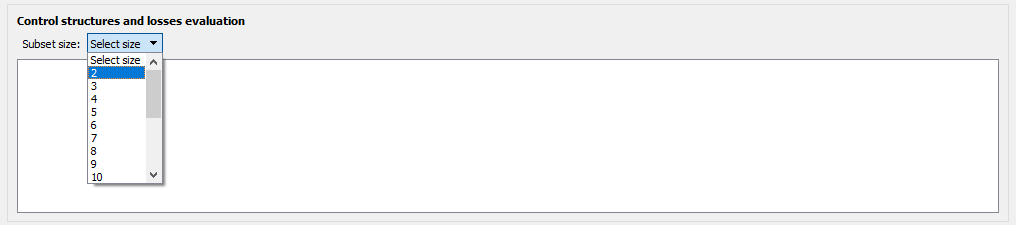
../_images/soc_analyze_subset.png

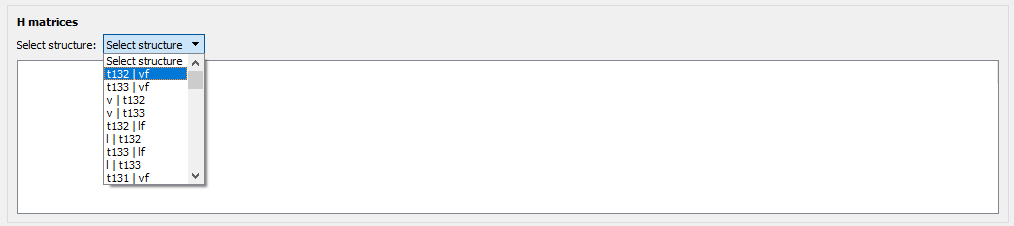
The linear combinations generated for the possible control structures:

../_images/soc_h_matrix.png

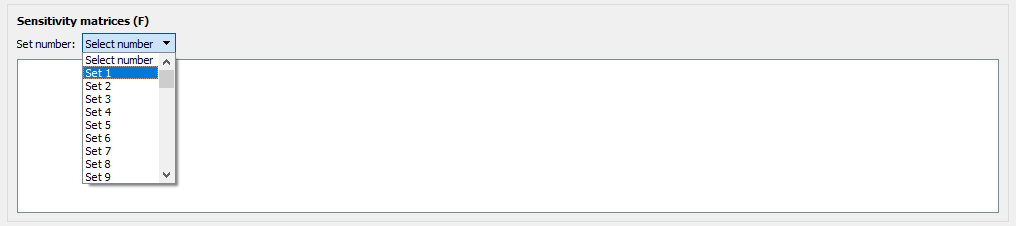
And the sensitivity matrices for each possible control structure evaluated:

../_images/soc_f_matrix.png

In addition, you can arrange the control structures in ascending and descending loss value order, to ease your study:

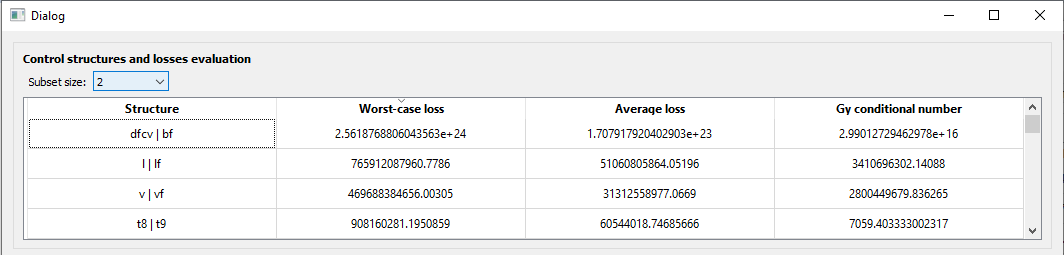
../_images/soc_ascending_size2.png
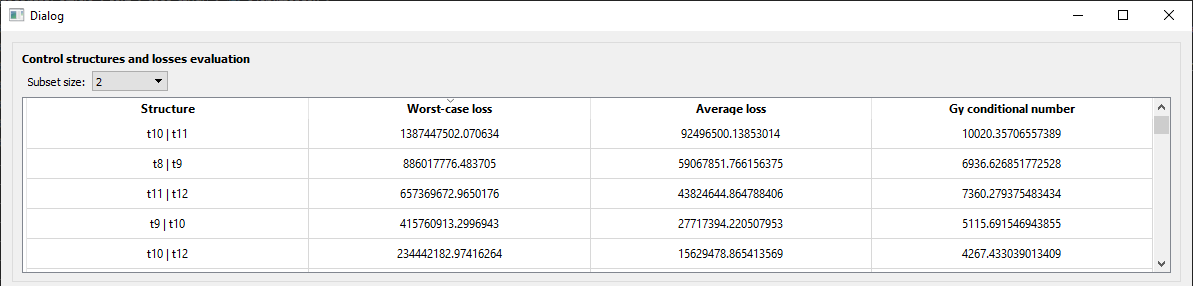
../_images/soc_descending_size2.png

For any subset size! For example, linear combinations of 6 measurements for this particular case shown here for illustration purposes:

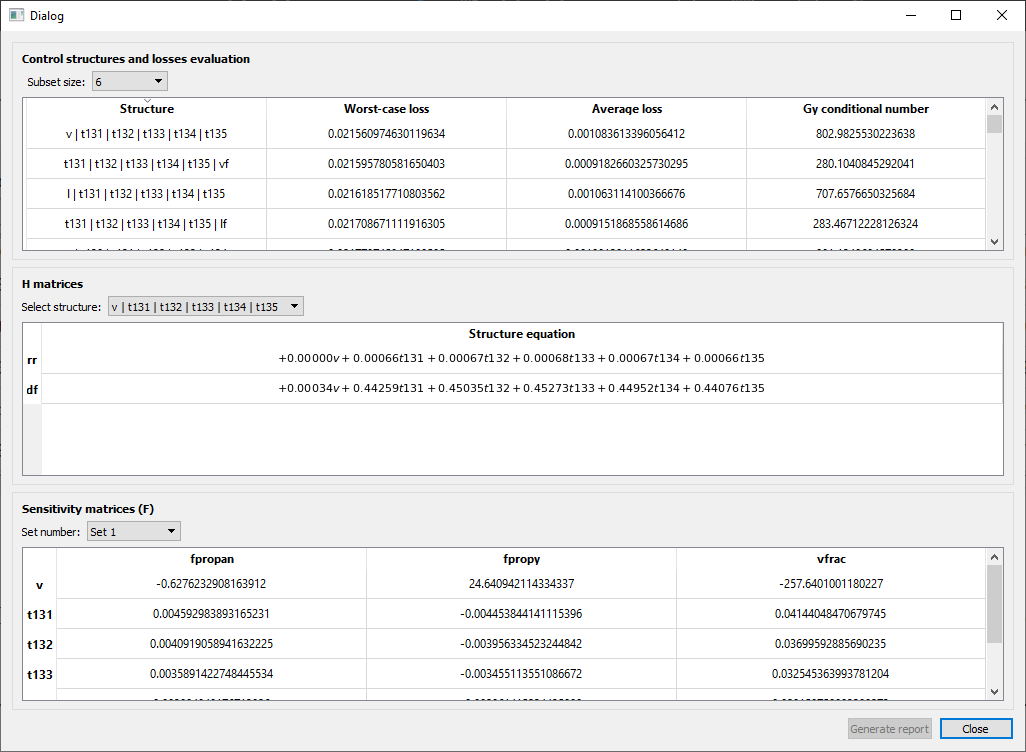
../_images/soc_size6.png

And inspect other controllability measures, such as the condition number (highlighted with a black-box):

../_images/soc_condition_number.png